В равнобокой трапеции высота, проведенная из вершины угла, равного 150 градусов, делит большее основание на отрезки 4 см и 12 см. Найдите площадь трапеции.

Решение1: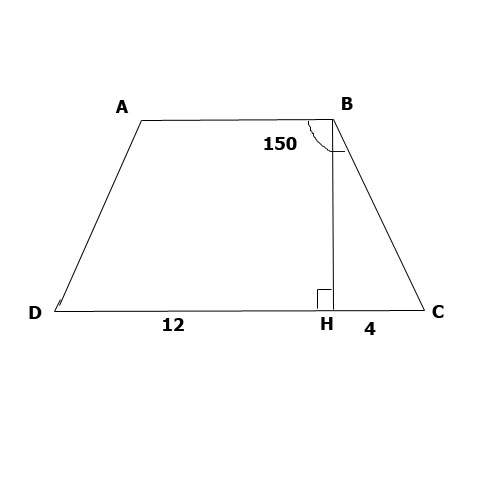

Высота, проведенная из угла 150 гр, отрезает от трапеции прямоугольный треугольник, в котором один из углов прямой, а второй равен 30 гр (при одной боковой стороне сумма углов у трапеции = 180, один угол =150 , соответственно второй=30).

найдем гипотенузу прямоугольного треугольника, которая для трапеции будет являться боковой стороной. Найти ее мы можем через синус угла = 60 гр.

sin = противлежащий катет/гипотенузу.

sin60=4/гипотенузу

Гипотенуза неизвестна, остальное известно. Выразим гипотенузу:

гип=4/sin60 = 8/√3

В прямоугольном треугольнике напротив угла 30 гр лежит катет, равный половине гипотенузы,

значит второй катет равен 4/√3

S трапеции = (a+b)h/2

где а и b  - основания трапеции

Второе основание найдем через первое. Если первое большее основание  равно 12+4=16, то второе основание мы найдем, опустив обе высоты с углов по 150 гр, они будут отсекать от основания по 4 см, значит меньшее основание = 16-(4*2)=8 см.

Подставим

S=(8+16)* 4/√3 /2=48см.кв.

Решение2:

По свойству углов в четырёхугольнике найдём углы при основании. Итак, трапеция ABCD, где BH - высота и угол при основании равен 30 градусов, можно рассмотреть треугольник ABH: угол A равен 30 градусов, сторона AH равна 4, находим гипотенузу

cos30* = 4/AB; √3/2 = 4/AB, получаем AB = 8/√3. По теореме Пифагора находим высоту BH. BH = (8/√3)^2 - 4^2;

64/3 - 48 = 16; BH = 4 (от корня в знаменателе избавляются при возведении в квадрат)

Итак, Если опустить высоту и из угла С, то треугольники получившиеся будут равны, стороны по 4 отсекаюся, получается, что BC = 8. По формуле для трапеции находим: S = 1/2(16+8) * 4 = 48 см^2