Задача №4

Даны две противоположные вершины квадрата А (-1;3) и С (6;2). Составить уравнение его сторон.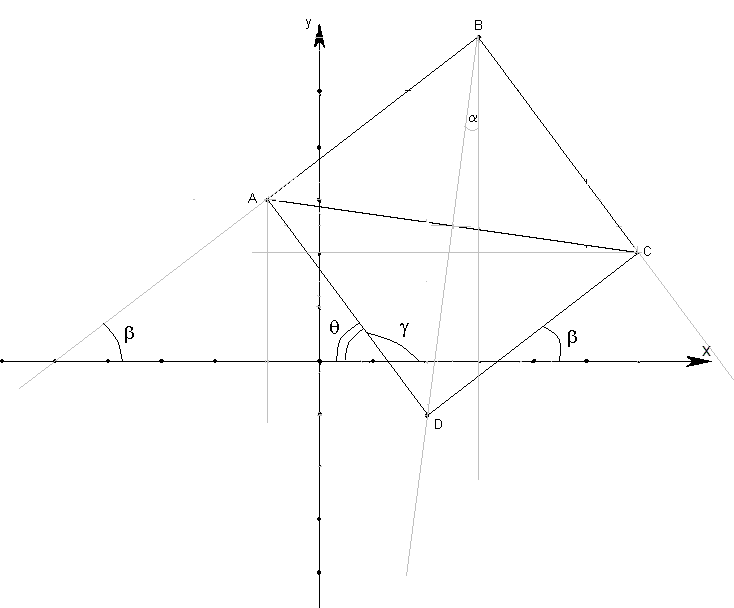

Уравнение прямой в плоскости y = kx + b

 

Для начала сделаем предположительное построение квадрата. Пусть точка В лежит сверху, а D снизу.

 

Мы видим, что диагональ BD – не перпендикулярна оси х, а немного отклонена. Обозначим угол отклонения за a.

 

Теперь рассмотрим угол b - угол между АВ и осью х. Если бы диагональ BD была перпендикулярна оси х, то угол b был бы равен 45°, но BD отклонена на угол a, значит, угол b = 45° - a. Коэффициент k в уравнении стороны АВ равен tgb. По формуле тангенса разности находим tgb = tg(45° - a) = ?. Необходимо заметить, что сторона CD параллельна стороне АВ и имеет с осью х аналогичных угол. Уравнения этих сторон различны лишь свободным членом. Запишем эти уравнения

у_АВ=3/4х+b_AB  для нахождения свободного члена необходимо подставить значения любой точки этой прямой. У нас она одна известна - это  точка А. Подставим значения и получим, что b_AB = 15/4. 

у_АВ=3/4х+15/4

у_CD=3/4х+b_CD  аналогично и тут только подставляем значения любой точки этой прямой то есть точки С. Подставим значения и получим, что b_CD = 5/2.    

у_CD=3/4х+ 5/2 

 

Теперь обратимся к сторонам BC и AD. Они параллельны, то есть образуют с осью х одинаковый угол. Обозначим его за g(гамма). Угол  g смежен с углом q (тетта), то есть g = 180° -q. А угол q в свою очередь равен q = 90° - b, подставим и получим g = 90° + b

Коэффициент k в уравнении сторон BC и AD равен tgg. tgg = tg(90° + b) = -ctgb = -4/3

Запишем эти уравнения

у_AD=-4/3х+b_AD  для нахождения свободного члена необходимо подставить значения любой точки этой прямой. У нас она одна известна - это  точка А. Подставим значения и получим, что b_AB = 5/3.

y_AD =-4/3х+5/3

y_BC=-4/3х+b_BC  аналогично и тут только подставляем значения любой точки этой прямой то есть точки С. Подставим значения и получим, что b_CD = 10. 

y_BC=-4/3х+ 10