Ребро правильного тетраэдра DABC равно а. Постройте сечение тетраэдра, проходящее через середины ребер DA и AB параллельно ребру BC, и найдите площадь этого сечения.

Решение:

Тетраэдр называется правильным, если все его грани — равносторонние треугольники.

Сечение пройдет через середины ребер АD и АВ по линии D1B1– это средняя линия ? АВD.

Сечение, параллельное ВС - проходит через В1С1 – среднюю линию ? АВС. 

Каждая сторона построенного сечения - средняя линия треугольника. ограничивающего грань тетраэдра, и по свойству средней линии  равна а/2, 

т.е. проведенное через середины ребер сечение - правильный треугольник со сторонами, равными а/2

Его площадь найдем по формуле площади равностороннего треугольника:

    S=(a?v3):4  

S=(a/2)?v3):4=(a?v3):16

_______________

Вариант решения:

Треугольник. получившийся в сечении, подобен треугольнику  ВСD с коэффициентом подобия

 k=( а/2):а=1/2

Отношение площадей подобных фигур равно квадрату коэффициента их подобия. 

S1:S=k?=1/4

S ?CDB=(a?v3):4

S сечения в 4 раза меньше и равно (a?v3):16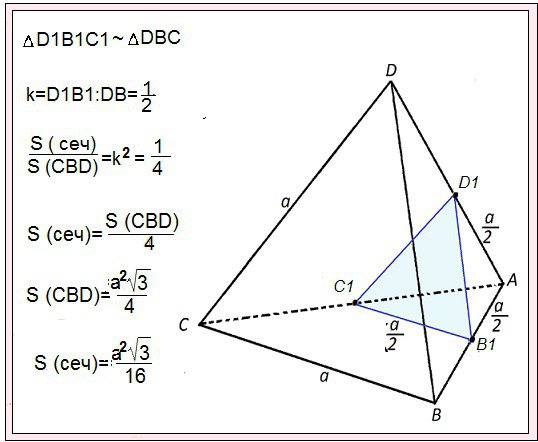