Точки M, N и K - середины ребер AD,BC и AB тетраэдара ABCD. На продолжении AN за точку N взята точка P так, что AP=2AN. Через точку P проведена прямая, параллельная плоскости DKC и пересекающая прямую CM в точке Q. Найдите отношение CQ:CM.

Решение: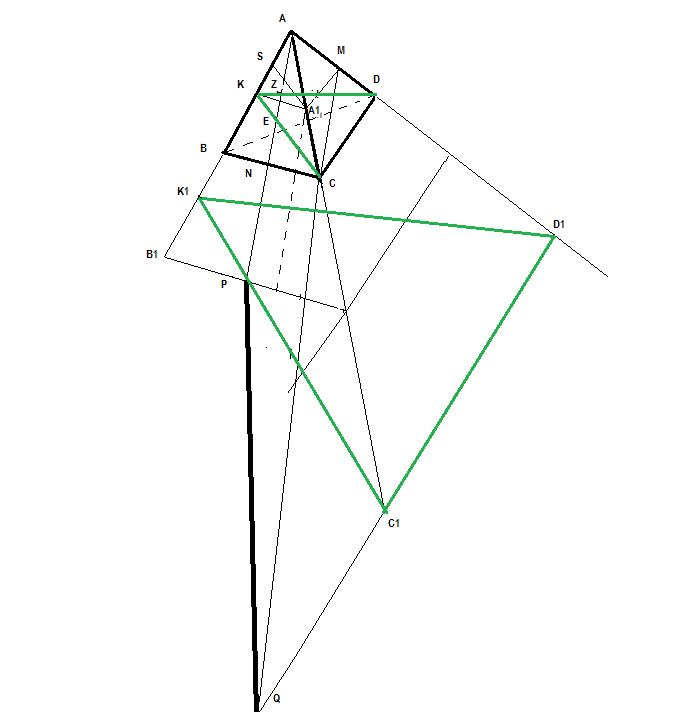

Проведем  дополнительные построения.

Продлим лучи AB,AC,AD.

В плоскости (ВАС) через  точку Р проведем прямую (К1С1) || (KC).

В плоскости (САD) через  точку С1 проведем прямую (С1D1) || (CD).

Плоскость (K1C1D1) параллельна (KCD) и проходит через точку Р.

Прямая (C1D1) - линия пересечения плоскостей (АС1D1) и (K1C1D1).

Прямая (MC) пересекает (C1D1) в точке Q.

Точка Q принадлежит плоскостям (АС1D1) и (K1C1D1).

Прямая (PQ) - искомая прямая, которая проходит через точку Р, Параллельная плоскости (DKC) и пересекающая прямую (СМ) в точке Q.

Теперь отношение CQ:CM

В ?ACD построим среднюю линию (MA1) || (CD), тогда |АА1| = |СА1|.

В ?ABC построим прямую (SA1) || (KC) || (K1C1).

Указанные прямые по теореме Фалеса отсекают на сторонах углов < BAN и <NAC

-пропорциональные отрезки.

Точка Е – пересечение медиан, отрезки |NE|=1/3*AN, |AE|=2/3 *AN.

Точка Z – пересечение (АЕ) и (SA1), отрезки |EZ|=|AZ|=1/3*AN.

Тогда PE:EZ=(PN+NE):EZ=(AN+1/3*AN):1/3*AN=4/3*AN:1/3*AN=4:1

?QCC1 и ?MCA1 – подобные по трем углам.

CQ:CM=CC1:CA1=PE:EZ=4:1

Ответ: отношение CQ:CM=4:1