В круге радиуса R проведены по одну сторону центра две параллельные хорды, из которых одна стягивает дугу в 120°, а другая в 60°. Определить часть площади круга, заключённую между хордами.

Решение:

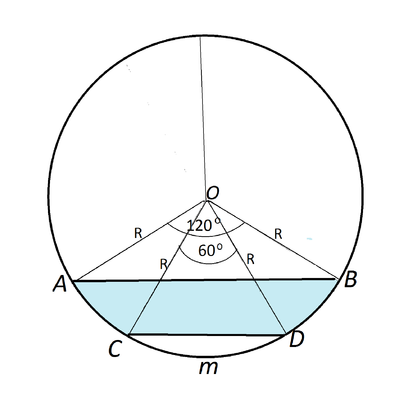
Рассмотрев рисунок, увидим, что фрагмент САВD- это сектор а ОАmВ  без   площадей треугольника АОВ и  сегмента СmD
S CABD=?R?:3-(S?AOB+S CmD)
Площадь сектора ОАmВ с дугой АmВ=120° равна 1/3 площади данного круга.  
Площадь сектора ОСmD с дугой  СmD=60° равна 1/6 площади круга
Площадь круга=?R?
Одной из формул площади равнобедренного треугольника является 
 S?=(a?*sin?):2
SCABD=?R?:3-S?AOB - S сегмента CmD
Стороны треугольника АОВ равны R
S ? AOB=R?*sin(120°):2= (R?√3):4
S сегмента CmD= Sсектора OCmD-S?COD
S сектора OCmD=?R?:6
Стороны треугольника СОD равны R
S ? COD=R?*sin(60°)=(R?√3):4
S CmD=?R?:6-(R?√3):4
SCABD=?R?:3-{(R?√3):4+?R?:6-(R?√3):4}
SCABD=?R?:3-(R?√3):4-?R?:6+(R?√3):4
SCABD=?R?:3-?R?:6+(R?√3):4-(R?√3):4
SCABD=?R?:3-?R?:6=?R?:6  
Ответ: часть площади круга между хордами равна 1/6 круга.