Биссектрисы острых углов равнобедренной трапеции пересекаются в точке, лежащей на меньшем основании. Большее основание равно 16, а боковая сторона 6. Найти среднюю линию трапеции.

Решение:

Из точки пересечения биссектрис (на верхнем основании) и из вершины малого основания опустим высоты на большое основание, угол при основании обозначим Ф.

Тогда

h = (16/2)*tg(Ф/2);

h = 6*sin(Ф);

Поэтому 6*sin(Ф) = 8*tg(Ф/2); дальше сплошная тригонометрия. :)))

12*sin(Ф/2)*cos(Ф/2) = 8*sin(Ф/2)/cos(Ф/2);

(cos(Ф/2))^2 = 2/3; Поэтому cos(Ф) = 2*(2/3) - 1 = 1/3;

На самом деле уже все решено, потому что

(а - b)/2 = 6*cos(Ф); а и b -основания,а = 16; Отсюда b = 12, а средняя линяя 14. 

 

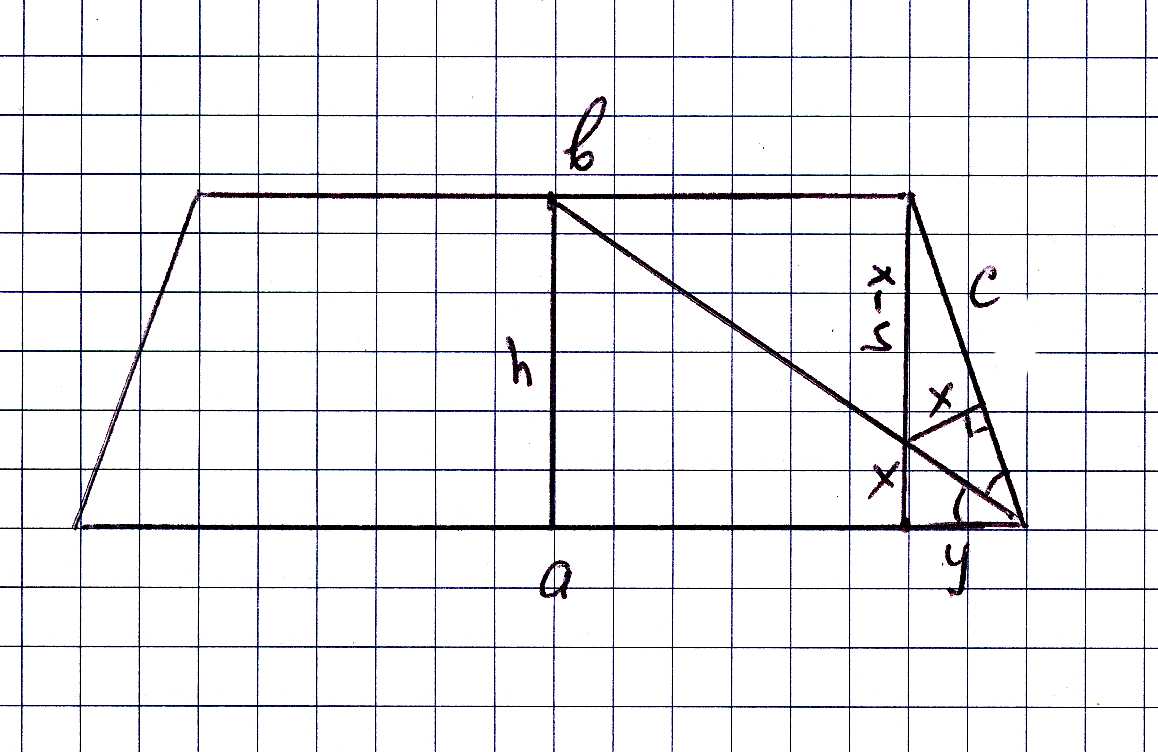
Поскольку нужно решить без тригонометрии, можно поступить по-другому. Смотрите чертеж, там все надписано, одна высота из точки пересечения биссектрис, другая - из вершины малого основания.

По свойству биссектрисы

(h - x)/x = c/y; 

Из подобия треугольников 

x/y = h/(a/2) = 2*h/a; выражаем отсюда x, подставляем в первое равенство

(h - (2*h/a)*y)/((2*h/a)*y)= c/y;

Откуда y = a/2 - c; очень простой ответ.

Итак, у = 8 - 6 = 2, как и в первом решении, y = (а - b)/2, b = 12,

Средняя линяя  = 14