Задача №79

Через точку А бокового ребра пирамиды проведена плоскость, параллельная плоскости основания, причем точка А делит ребро на два отрезка, длины которых находятся в отношении 1:3, считая от вершины. Найдите объем пирамиды, если объем образовавшейся усеченной пирамиды равен 315 см в кубе.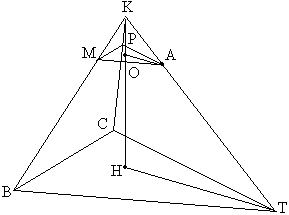

1.
Плоскость, пересекая грани пирамиды, задает треугольник, стороны которого соответственно параллельны сторонам треугольника ВСТ (основания). То есть: МА || ВТ; РА || СТ; МР || ВС
Рассмотрим грань ВКТ. В следствии параллельности ВТ и АМ равны углы: угол КВТ = углу КМА и угол КТВ = углу КАМ. Из равенства этих углов следует подобие треугольников КМА и КВТ. Отсюда следует, что МА:ВТ = КА:КТ
Нам известно, что КА:АТ = 1:3, значит, КА:КТ = 1:4. Отсюда МА:ВТ = 1:4.
Угол ВТС равен углу МАР (эти углы связаны параллельным переносом. ТВ перешло в АМ, а ТС - в АР)
Заключаем, что треугольники ВСТ и АМР подобны по двум сторонам и углу между ними. Как известно коэффициент подобия площадей фигур равен квадрату коэффициента подобия соответственных сторон. Поэтому, обозначив площадь треугольника ВСТ за S₁, а площадь треугольника АМР за S₂, можно записать следующее соотношение:
S₁ = 16S₂
2.
Прямоугольные треугольники КОА и КНТ подобны по острому углу при вершине К. Поэтому КА:КТ = КР:КН. Как известно КА:КТ = 1:4, значит, КР:КН = 1:4. Откуда КР = (1/4)*КН. Если так, то РН = (3/4)*КН.
3.
Запишем формулу усеченной пирамиды для нашего случая:

Заменим: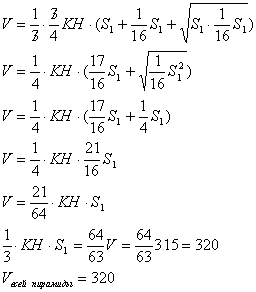