Задача №82

Боковое ребро правильной четырехугольной пирамиды составляет с основанием угол a. А середина этого ребра удалена от основания на расстояние m. Найти объем пирамиды.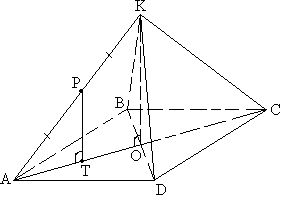

1.
а).
Так как пирамида правильная, то углы КАВ и КАD равны. Основание АВСD - квадрат. Угол КАО есть α.
Теорема. Пусть даны три пересекающиеся прямые, не лежащие в одной плоскости. Опустим перпендикуляр из свободного конца одной из прямых на плоскость, образованную двумя друними прямыми. Этот перпендикуляр упадет на биссектрису угла, образованного двумя друними прямыми тогда и только тогда, когда данная прямая образует с двумя друними прямыми равные углы.
Теорема. Диагонали ромба (в частном случае квадрата) являются биссектриссами его углов и пересекаются под прямым углом.
Исходя из этих теорем, определяем, что перпендикуляр РТ падает на АС.
б).
Прямоугольные треугольники АКО и АРТ подобны по острому углу КАО, причем АК = 2АР по данным. Значит:
АО = 2АТ и КО = 2РТ = 2m
в).
Из прямоугольного треугольника АРТ:
АТ = РТ*ctgα, значит,
АО = 2АТ = 2m*ctgα
АС = 2АО = 4m*ctgα
Найдем площадь основания - квадрата по имеющейся диагонали:
S = AC²/2 = 8m²*ctg²α

2.
а).
По имеющейся высоте КО и площади основания S найдем объем пирамиды: