Задача №83

Дан прямоугольный параллелепипед. Его диагональ равна 5 корней из 2. Угол между диагональю параллелепипеда и его основанием равен 45 градусам. Площадь основания равна 12. Найти площадь боковой поверхности параллелепипеда.

1.
а).
Рассмотрим треугольник АРС: он прямоугольный с острым углом 45 градусов, т.е. он равнобедренный и его катеты меньше гипотенузы в корень из 2 раз. То есть катеты равны 5.
б).
Рассмотрим основание АВСD: его площадь известна. Здесь известна диагональ, она равна 5. Запишем формулу площади прямоугольника через диагонали: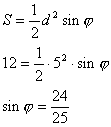

в).
Рассмотрим треугольник АОВ. В нем АО = ОВ = d/2. Значит, он равнобедренный, и высота ОР является также и медианой, и биссектриссой. Тогда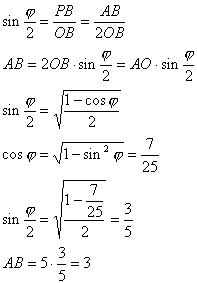

г).
Запишем формулу площади основания АВСD: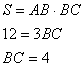

2.
а).
Противолежащие грани параллелепипеда равны, поэтому формула площади выглядит так: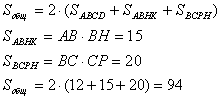