| Главная Онлайн-расчеты Научный калькулятор | |
Задача №9Даны уравнения двух сторон параллелограмма 8х+3у+1=0, 2х+у-1=0 и уравнение одной из его диагоналей 3х+2у+3=0. Определить координаты вершин этого параллелограмма.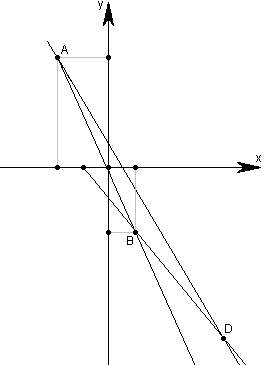
Выразим у: 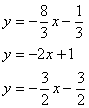
Мы видим, что в уравнениях сторон коэффициенты при х не равны, значит прямые, определяемые этими уравнениями, не параллельны. То есть пересекаются, образуя одну из вершин. Пусть это будет вершина А. И пусть первое уравнение – сторона АВ, второе – АD. Для нахождения точки А приравняем эти два уравнения: 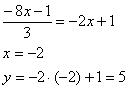
А(-2;5) Мы видим, что уравнение 3х+2у+3=0 задает диагональ BD. Поэтому, приравняв сначала 1 и 3, а затем 2 и 3 уравнения, найдем соответственно точки D и В. 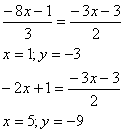
Итак В(1;-3) D(5;-9) Как известно в параллелограмме противоположные стороны параллельны, то есть коэффициенты k при х равны. Поэтому для сторон ВС и CD остаются неизвестными только свободные члены d. Найдем их, подставив в уравнения прямых их известные точки D и В соответственно: 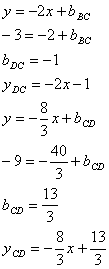
Теперь для нахождения точки С приравняем уравнения сторон BC и CD 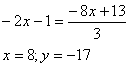
С(8;-17) |
|