Задача №94

Вершины четырехугольника АВСD делят окружность в отношении 1:2:8:7.Найдите углы этого четырехугольника.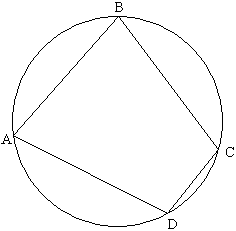

Нам известно отношение длин дуг, на которые вершины четырехугольника делят окружность. Также известно, что длина дуги прямо пропорциональна углу, операющемуся на эту дугу. Поэтому углы находятся в одинаковом отношении.
Пусть данные дуги равны: DC = x; AD = 2х; BC = 8x; AB = 7x
Угол В опирается на дугу АС, которая равна сумме дуг АD и DC: AC = АD+DC = 3x
Подобно этому: для угла А - BD = 9x; для угла С - BD = 9x; для угла D - АС = 15x
Теорема. Сумма углов четырехугольника равна 360^о.
Поэтому:
3х+9х+9х+15х=360,
откуда х = 10 исходя из этого получаем:
В = 3х = 30^о
А = 9х = 90^о
С = 9х = 90^о
D = 15х = 150^о