Задача №97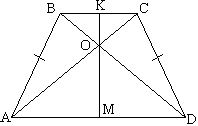

Задачи по геометрии

Докажите, что в равнобокой трапеции диагонали равны и точка пересечения диагоналей лежит на оси симметрии.

Теорема. Углы, прилежащие к основаниям трапеции, равны.
Поэтому треугольники АВD и АСD равны по двум сторонам и углу между ними (АВ=CD - трапеция равнобокая, AD - общая, углы А и D равны по теореме).
Из равенства треугольников следует равенство соответствующих сторон: АС=BD и углов: ∠ВАD=∠ВDА
Равенство этих углов и
Теорема. Если в треугольнике два угла равны, то он равнобедренный, и сторона, к которой прилежат равные углы есть основание, а две другие боковые.
говорят нам, что треугольник АОD равнобедренный, поэтому перпендикуляр, опущенный из точки О на основание AD, делит его попалам. Этот перпендикуляр совпадает с осью симметрии, т.к.
Теорема. Из любой точки прямой можно восстановить перпендикуляр, причем только один.
а следовательно и точка О - пересечение диагоналей - принадлежит оси симметрии трапеции.