Вписанная, описанная и вневписанная окружности

Рассмотрим окружность, вписанную в треугольник.
Определение 9. Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Теорема 36. Центр вписанной в треугольник окружности лежит на пересечении биссектрис внутренних углов треугольника.

Доказательство: Действительно, вписанная в треугольник ABC окружность с центром в точке O касается всех сторон треугольника по определению вписанной окружности. Это значит, что точка O удалена от сторон треугольника ABC на расстояние, равное радиусу вписанной окружности, то есть точка O равноудалена от сторон треугольника ABC. Следовательно, точка O равноудалена от сторон AB и AC, то есть лежит на биссектрисе угла A. Аналогично точка O лежит на биссектрисе углов B и C. Теорема доказана.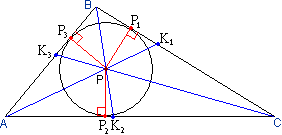
Мы знаем, что центр окружности равноудален от всех точек окружности (по определению) в том числе и от точек касание сторон треугольника. Также мы знаем, что каждая точка биссектрисы угла равноудалена от сторон угла. А точка пересечения биссектрис треугольника равноудалена от каждой стороны, т.к. равноудалена от трех пар сторон для кадой биссектрисы. Таким образом, в треугольнике есть только одна точка равноудаленная от всех сторон - это пересечение биссектрис треугольника. Поэтому центр лежит именно в этой точке.
Теорема 36.1. В любой треугольник можно вписать окружность, и только одну.
В каждый треугольник можно вписать окружность, т.к. в каждом треугольнике есть точка равноудаленная от его сторон - точка пересечения биссектрис.
Отрезки РА, РВ, РС, соединяющие Р с вершинами треугольника АВС, разобьют треугольник на три треугольника АВР, АСР и ВСР. Высота каждого из этих треугольников  равна радиусу вписанной окружности, и потому их площади выражаются как S₁=1/2rc, S₂=1/2ra, S₃=1/2rb.
Площадь всего треугольника АВС равна сумме этих площадей, и отсюда выводим радиус: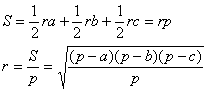
(1)
где р – полупериметр треугольника.
Теорема 37. Радиус вписанной в треугольник окружности равен отношению площади треугольника и его полупериметра.
Рассмотрим окружность, описанную около треугольника:
Определение 10. Окружность называется описанной около треугольника, если она проходит через три его вершины.
Определение 11. Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Теорема 38. Серединные перпендикуляры трех сторон треугольника пересекаются в одной точке.

Доказательство: Прямая QO - серединный перпендикуляр к стороне AB треугольника ABC. Прямая PO - серединный перпендикуляр к стороне BC. Эти две прямые пересекаются в точке O (действительно, пусть они не пересекаются; тогда они параллельны, а значит, угол ABC развернутый; это означало бы, что точки A, B и C лежат на одной прямой, а это противоречит определению треугольника). Итак, серединные перпендикуляры к сторонам AB и BC пересекаются в точке O. Тогда точка O равноудалена от точек A, B и C. Значит, AO = OC. Следовательно, точка O принадлежит геометрическому месту точек, равноудаленных от концов отрезка AC, то есть лежит на серединном перпендикуляре к этому отрезку. Значит, точка O принадлежит всем трём серединным перпендикулярам к сторонам треугольника ABC, то есть является точкой их пересечения. Значит, эти серединные перпендикуляры пересекаются в одной точке. Теорема доказана.
Теорема 38.1. Точка пересечения серединных перпендикуляров к сторонам треугольника равноуда-лена от его вершин.
Теорема 39. Точка пересечения серединных перпендикуляров треугольника является центром описанной около треугольника окружности.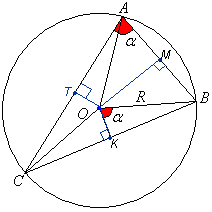

Доказательство: Пусть ABC - данный треугольник, а O - центр описанной около него окружности. Окружность проходит через точки A, B, C. Значит, OA = OB = OC, то есть OAB, OBC, OAC - равнобедренные треугольники. Точка O равноудалена от концов отрезков AB, BC, AC. Следовательно, точка O принадлежит геометрическому месту точек, равноудаленных от концов отрезка AB, геометрическому месту точек, равноудалённых от концов отрезка BC, а также геометрическому месту точек, равноудалённых от концов отрезка AC. Значит, точка O принадлежит серединному перпендикуляру к AB, серединному перпендикуляру к BC, а также серединному перпендикуляру к AC. Теорема доказана.
Теорема 39.1. Вокруг любого треугольника можно описать окружность, и только одну.
Теорема 40. В любом треугольнике сторона равна произведению диаметра описанной окружности и синуса противолежащего угла.
Доказательство. Рассмотрим произвольный треугольник АВС и описанную около него окружность, радиус которой обозначим через R. Пусть А – острый угол треугольника. Проведем радиусы ОВ, ОС окружности и опустим из её центра О перпендикуляр ОК на сторону ВС треугольника. Заметим, что угол a треугольника измеряется половиной дуги ВС, для которой угол ВОС является центральным углом. Отсюда видно, что ?ВОС=2a, а ?СОК=a. Поэтому из прямоугольного треугольника СОК находим что и требовалось доказать.
Приведенные рассуждения относятся к случаю острого угла треугольника; нетрудно было бы провести доказательства и для случаев прямого и тупого угла, но можно использовать теорему синусов. Так как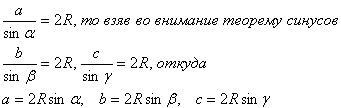
(3)

Т.е. теорему синусов можно записать так: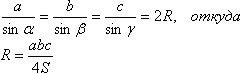

(4)

(5)

Формула 5 исходит из теоремы
Теорема d6. Площадь треугольника равна отношению произведения длин всех его сторон к учетверенному радиусу окружности, описанной около этого треугольника.
Доказательство: По теореме 40, 2Rsinα = a. Следовательно, R·2bc·sinα = abc. Но 2bc sinα = 4S, а значит, 4RS = abc. Следовательно, S = abc / 4R. Теорема доказана.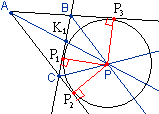

Существуют, однако, еще три окружности, касающиеся всех трех прямых, на которых лежат стороны треугольника. Так, рассмотрим треугольник АВС и биссектрисы его внутреннего угла А и двух внешних углов В и С:
Точка пересечения последних двух биссектрис одинаково удалена от всех трех прямых АВ, ВС и АС и потому лежит на биссектрисе угла А; она является центром окружности, касающейся стороны ВС треугольника и продолжений двух других его сторон. Такая окружность называется внешне вписанной (вневписанной) в треугольник.
Определение 12. Окружность, касающаяся одной стороны треугольника и продолжений двух других его сторон, называется вневписанной.
Теорема 41. Центр вневписанной окружности лежит на пересечении биссектрис внешних углов, при вершинах касаемой стороны, и биссектрисы угла при третей вершине.