Теорема косинусов

Рассмотрим сторону b  треугольника АВС, лежащую против угла b. Вычисление длины этой стороны проведем отдельно в двух случаях, когда угол b острый и когда угол b тупой.
1) Угол b - острый (рисунок 1). Проведем в треугольнике АВС высоту СН = h. Отрезок ВН, который является проекцией стороны ВС на АВ, обозначим через l. Тогда отрезок АН выразится как c – l. Применим теорему Пифагора к каждому из двух треугольников АНС и ВНС, на которые данный треугольник разбивается высотой СН. Получим
b² = h² + (c – l)², h² = a² – l².
Подставляя h² из второго равенства в первое, найдем
b² = a² + c² – 2lc(1)
Теорема 28. Квадрат стороны треугольника, лежащей против острого угла, равен сумме квадратов двух других сторон треугольника минус удвоенное произведение одной из них на проекцию на неё другой стороны.
2) Угол b - тупой (рисунок 2). Проведем в треугольнике АВС высоту СН = h. Отрезок ВН, который является проекцией стороны ВС на АВ, обозначим через l. Тогда отрезок АН выразится как c + l.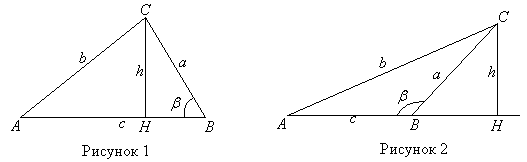

Применим теорему Пифагора к каждому из двух треугольников АНС и ВНС, на которые данный треугольник разбивается высотой СН. Получим
b² = h² + (c + l)², h² = a² – l².
Подставляя h² из второго равенства в первое, найдем
b² = a² + c² + 2lc(2)
Теорема 29. Квадрат стороны треугольника, лежащей против тупого угла, равен сумме квадратов двух других сторон треугольника плюс удвоенное произведение одной из них на проекцию на неё другой стороны.
Теорема 30 Квадрат стороны, лежащей против острого (тупого) угла, меньше (больше) суммы квадратов двух других сторон треугольника. Равенство имеет место для стороны, лежащей против прямого угла.
Формулам, которые мы только что получили, можно придать единообразную форму, используя выражение проекции l через косинус угла b. Именно, в случае острого угла b непосредственно имеем l=acosb. В случае тупого угла b проекция l выражается из треугольника ВСН как l=acos(p-b). Используя формулы приведения, получим l=-acosb. Теперь видно, что заменяя l в данных формулах получим одно и то же равенство:
b²=a²+c²-2accosb(3)
Теорема 31. Теорема Косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон и косинуса угла, заключенного между ними.
С помощью теоремы косинусов может быть доказана
Теорема 32. Если в двух треугольниках имеются две пары равных сторон, то третья сторона больше в том треугольнике, где она лежит против большего угла.
Доказательство. Из формулы видно, что при постоянных длинах сторон а и с сторона b будет тем больше, чем меньше cosb; так как при возрастании аргумента его косинус монотонно убывает, то справедливость нашего утверждения доказана