Задача №117

Доказать, что сумма квадратов всех медиан треугольника составляет 3/4 от суммы квадратов его сторон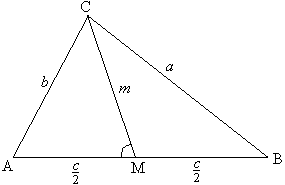

Для начала найдем длину медианы треугольника, например проведенной из вершины С. Обозначим длины сторон, лежащих против вершин А,В и С, соответственно a, b, c.
Пусть СМ - медиана треугольника АВС. Обозначим СМ=m, ∠СМА=α, тогда ∠СМВ=180^о - α
Из треугольников АСМ и СМВ по теореме косинусов будем иметь: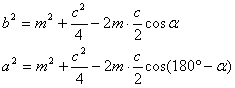

Складывая почленно два этих равенства и учитывая, что cos(180^о - α)=-cosα, получаем: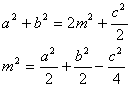

Теперь сделаем следующие обозначения: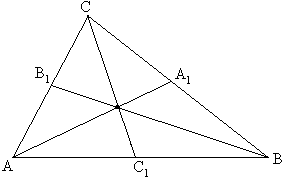

Запишем полученное выражение для каждой медианы: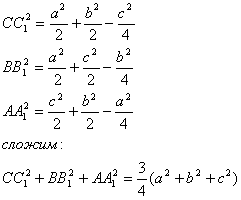