Главная       Онлайн-расчеты       Научный калькулятор

Задача №141

Через внешнюю точку к окружности проведены секущая, проходящая через центр окружности, и касательная, отрезок которой до точки касания равен половине секущей. Докажите, что отрезок касательной относится к радиусу окружности как 4:3.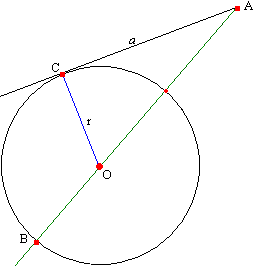
рисунок к задаче 141 №1 Обозначим отрезок касательной за а, тогда секущая будет равны 2а. Радиус окружности обозначим за r, тогда АО = 2а - r. Для треугольника АОС запишем теорему Пифагора: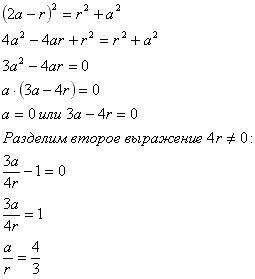
вычисления