Задача №148

В правильной четырехугольной пирамиде диагональ основания равна 12 см, угол наклона боковых граней 60 градусов. Через середину высоты и вершину основания проведено сечение параллельно диагонали основания. Найти площадь сечения.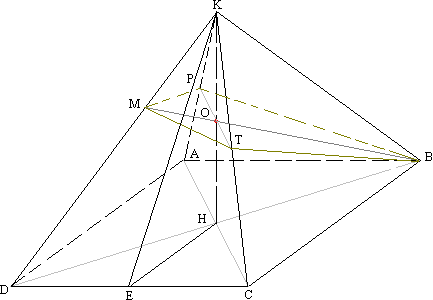

Построим сечение для вершины В и диагонали АС. Для этого в плоскости АКС через середину высоты КН проведем прямую РТ параллельно АС. Прямая РТ и точка В определяют плоскость и притом только одну. АС параллельна одной прямой плоскости РТВ, значит параллельна и всей этой плоскости. Таким образом, мы получили искомую плоскость. Достроим. В плоскости ВКD проведем прямую через точки О и В и продолжим её до пересечения с КD. Точка М принадлежит плоскости РТВ, т.к. принадлежит прямой ОВ этой плоскости.
Построим двугранный угол между основанием и боковой гранью. Для этого в грани KCD проведем высоту КЕ. Теперь соединим точки Е и Н. ЕН перпендикулярна CD по теореме о трех перпендикулярах, а угол КЕН - линейный угол двугранного угла между основанием и боковой гранью и равен 60 градусов.
Сторона квадрата в корень из двух раз меньше его диагонали. В прямоугольном треугольнике ЕКН: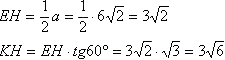

Из прямоугольного треугольника КНС: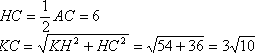

Рассмотрим треугольник KBD: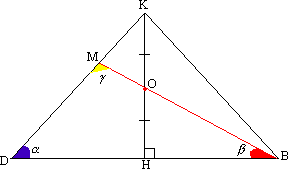

Здесь обозначим углы и вычислим их тригонометрические значения: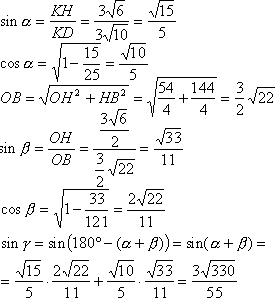

Теперь запишем теорему синусов:

Рассмотрим треугольник АКС, а именно угол АКН. Теорема: Параллельные линии отсекают на сторонах угла пропорциональные отрезки. Прямые АС и РТ параллельны по построению, и мы знаем, что точка О - середина КН, поэтому Р середина АК. Также и для угла СКН: Т - -середина СК. Поэтому РТ - средняя линия в треугольнике АКС и равна половине АС.
Теорема: Если в одной из двух перпендикулярных плоскостей проведена прямая, перпендикулярная их линии пересечения, то эта прямая перпендикулярна и все второй плоскости. Рассмотрим эту теорему для перпендикулярных плоскостей АВС и KBD и прямой АС (АС перпендикулярна BD, т.к. диагонали квадрата перпендикулярны). АС перпендикулярна KBD. Теорема: если одна из двух параллельных прямых перпендикулярна плоскости, то и вторая перпендикулярна этой плоскости. Поэтому РТ (РТ параллельна АС по построению) перпендикулярна плоскости KBD. А значит, перпендикулярна и любой прямой этой плоскости. РТ перпендикулярна ВМ. Другими словами угол меджу диагоналями четырехугольника ВТМР равен 90 градусов. Вычислим его площадь: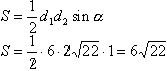