Задача №16

Доказать, что через точку Р (2,5) можно провести две прямые линии так, чтобы их расстояния от точки Q (5,1) были равны 3. Составить уравнения этих прямых.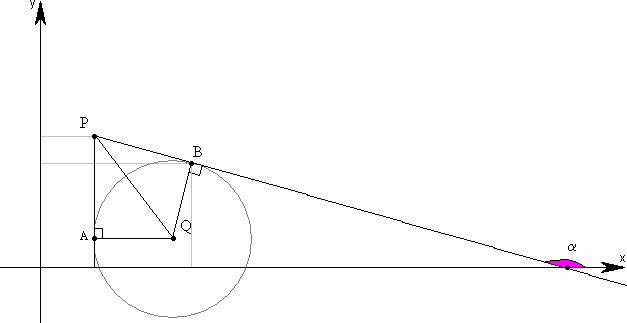

Построим окружность радиуса 3, взяв за центр точку Q. Теперь из точки Р проведем две касательные к полученной окружности и обозначим точки касания за А и В.

Как известно радиус перпендикулярен касательной в точки касания. Иными словами QA^AP и QB^BP или отрезки QA и QB являются расстояниями соответственно до прямых AP и BP. Заметим, что QA и QB являются радиусами построенной окружности и равны 3. Другими словами мы нашли две прямые AP и BP, расстояние до которых от точки Q равно 3.
Почему же больше нет прямых, расстояние до которых от точки Q равно 3. Да потому что из точки, лежащей вне окружности, можно провести к ней не более двух касательных.

Зная координаты центра окружности составим её уравнение:

(х-5)²+(у-1)²=9 (1)
Через точку Q проведем прямую параллельно оси Ох. Пусть она пересечет окружность в точке А. Раз прямая АQ параллельна оси, значит, точка А имеет координату у такую же как и у точки Q, т.е. 1.
Подставим это значение в выражение (1) и получим координату х точки А:
(х-5)²+(1-1)²=9
х-5=+3 или х-5=-3 - берем положительный результат (х=2), т.к. точка А лежит в первой четверти. таким образом А(2;1).
Замечаем, что точка А и точак Р имеют одинаковую координату х, т.е. прямая АР параллельна оси у. Это в свою очередь означает, что АР^QA (две пересекающиеся прямые, соответственно параллельные двум перпендикулярным прямым, перпендикулярны). Т.е. прямая АР перпендикулярна радиусу QA. Если радиус перпендикулярен прямой в точке пересечения ей окружности, то эта прямая - касательная к этой окружности.
Прямая АР параллельна оси Оу, и поэтому имеет уравнение х = 2.

Найдем PQ и АР по координанам концов: PQ=5; AP=4

Треугольники APQ и PBQ равны (по катету и гипотенузе), следовательно углы APQ и BPQ равны.

Найдем тангенс угла АРQ: tgAPQ=3/4, теперь найдем тангенс угла АРВ: tgАРВ=tg2∠АРQ=24/7 (формула 21)

Теперь найдем тангенс угла a, используя теорему о внешнем угле треугольника

tga=tg(90+∠АРВ)=-ctg∠АРВ=-1/tg∠АРВ =-7/24

Таким образом уравнение прямой РВ записывается

у=-7/24х+d. И для нахождения d подставим значения точки Р в это уравнение

5=-7/12+d, откуда d=67/12