Задача №173

В равнобедренном треугольнике центр вписанной в треугольник окружности делит высоту в отношении 5:2(считая от вершины), а длина боковой стороны 25см. Вычислить длину основания треугольника.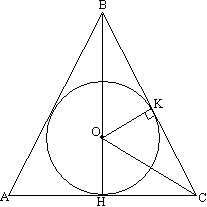
Нужно отметить, что имеется в виду высота основания, т.к. высоты боковых сторон не проходят через центр вписанной окружности, вернее проходят только в случае правильного треугольника, но в случае правильного треугольника отношение было бы 2:1 (св-во медиан).
Пользуясь тем, что радиус, проведенный в точку касания, перпендикулярен касательной, докажем, что ОК перпендикулярен ВС. Прямоугольные треугольники ОСН и ОСК равны по катету и гипотенузе (ОК=ОН - радиусы, ОС - общая), поэтому НС=КС.
ОВ=5х, ОН=ОК=2х, ВН=7х. В прямоугольном треугольнике ОВК найдем ВК:

Прямоугольные треугольники ВСН и ВКО подобны по острому углу (при вершине В), поэтому:
ОК:НС=ВК:ВН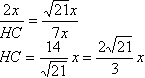

Теперь запишем теорему Пифагора для треугольника ВСН: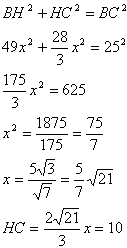

По свойству равнобедренного треугольника высота ВН являтеся также и медианой, поэтому АН=НС или АС=2НС=20