Задача №180

В параллелограмме АВСD угол при вершине А тупой, длина стороны ВС=17, СD=6, а площадь равна 90. Прямая, параллельная стороне АD, пересекает сторону АВ в точке Е, а диагональ ВD - в точке F. Длина отрезка ВЕ=2. Найти длину отрезка DF.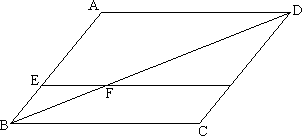
Запишем формулу площади параллелограмма:
S=a * b * sin∠А, откуда sin∠А=15/17
Через основное тождество найдем cos∠А=8/17
Для треугольника АВD запишем теорему косинусов:
BD²=AB²+AD²-2AB * AD * cos∠А
BD²=36+289-2 * 6 * 17 * 8/17
BD²=229
Треугольники АВD и EBF подобны по двум углам (∠В-общий, ∠ВЕF=∠BAD, как соответственные). Поэтому: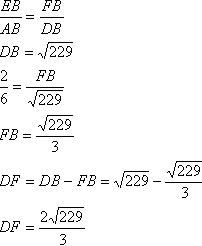