Задача №190

Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань-квадрат со стороной 6 корней из 2 см.
а) найдите площадь полной поверхности этой призмы;
б) постройте сечение призмы плоскостью, проходящей через катет нижнего основания и середину противолежащего бокового ребра;
в) вычислите площадь этого сечения;
г) найдите угол между плоскостью сечения и плоскостью нижнего основания;
д) постройте линию пересечения секущей плоскости верхнего основания.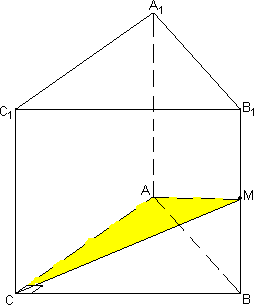
а) Призма прямая, т.е. её боковые ребра перпендикулярны основаниям. Боковые грани являются прямоугольниками. Площадь прямоугольника равна произведению длин смежных сторон, следовательно, площадь той грани больше, ребра которой больше. Боковые ребра параллелепипеда равны, а в основании самуую большую длину имеет гипотенуза, поэтому большая грань - ABB₁A₁.
И раз эта грань - квадрат, то все её стороны по 6 корней из 2, в том числе и гипотенуза основания. Пусть АС=ВС=х, из теоремы Пифагора найдем катеты основания и его площадь: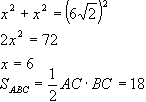

Теперь найдем площади боковых граней, а затем и площадь полной поверхности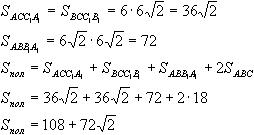


б) Соединим середину BB₁ точку М с точками А и С. Плоскость АМС и будет искомая.
в) По теореме о трех перпендикулярах МС перпендикулярна АС (МС-наклонная, ВС-проекция). Поэтому треугольник АМС прямоугольный.
Из прямоугольного треугольника МВС найдем МС по теореме Пифагора: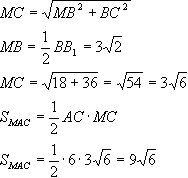


г) Угол МСВ является линейным углом двугранного угла между плоскостями АВС и МАС (по определению). Именно его нам нужно определить. Из прямоугольного треугольника МВС найдем косинус этого угла: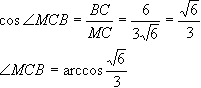


д) В плоскости СВВ₁С₁ продолжим С₁В₁ в сторону точки В₁. Также МС продолжим в сторону точки М до пересечения с С₁В₁. Точку пересечения обозначим за О.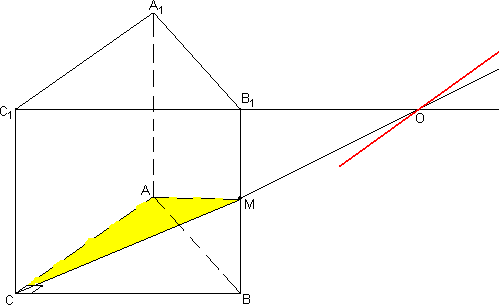

Эта точка принадлежит плоскости А₁В₁С₁, т.к. лежит на прямой В₁С₁, принадлежащей этой плоскости. Также точка О принадлежит плоскости МАС, т.к. лежит на прямой МС, принадлеащей этой плоскости. Значит, она лежит на прямой пересечения этих плоскостей.
Известно, что линии пересечения двух параллельных плоскостей (оснований призмы) третей плоскостью (МАС) параллельны. Через точку О проведем прямую параллельно прямой АС. Это и будет искомая прямая.