Задача №221

В прямоугольный треугольник вписан квадрат, имеющий с ним общий угол. Найти площадь квадрата, если катеты треугольника равны 10 и 15.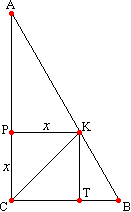
Обозначим сторону квадрата за х, тогда:
ТВ=10-х
АР=15-х
Запишем теорему Пифагора для треугольников АРК и КТВ:

Вспомним теорему: если точка равноудалена от сторон угла, то на принадлежит биссектрисе этого угла. Точка К равноудалена от сторо угла С, поэтому СК есть биссектриса. Воспользуемся теоремой 2 темы треугольник: Биссектриса внутреннего угла треугольника делит противолежащую сторону на части, пропорциональные прилежащим сторонам. В нашем случае это будет выглядеть так: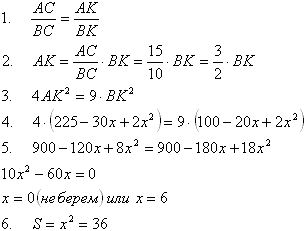


1. записали теорему
2. подставили известные величины
3. полученное выражение возвели в квадрат
4. подставили ранее найденные выражения
5. решили уравнение
6. нашли площадь квадрата как квадрат длины стороны