Задача №228

Длина окружности сечения шара плоскостью равна 6π. Расстояние от центра шара до плоскости сечения 3. Вычислите объем шара.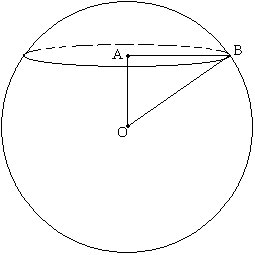
Итак, опустим перпендикуляр ОА на плоскость сечения. Отрезок ОА будет расстоянием от центра шара до плоскости сечения по определению, и поэтому ОА=3. Точка А является центром окружности-сечения
Это следует из того, что точка А равноудалена от всех точек этой окружности. Так, например, треугольники ОАВ и ОАС прямоугольны (т.к. ОА перпендикулярно плоскости сечения) и равны по катету и гипотенузе (ОА - общая, ОС=ОВ - радиусы шара).
Значит, АВ является радиусом сечения. Пусть радиус сечения - r, тогда по формуле длины окружности:
l=2πr=6π
r=3
1. Из прямоугольного треугольника АОВ по теореме Пифагора получаем: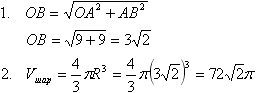

2. Нашли объем шара по формуле объема