Задача №237

В прямоугольной трапеции боковые стороны относятся как 4:5, разность оснований равна 9 см.,а меньшая диагональ равна 13см. Найти площадь трапеции.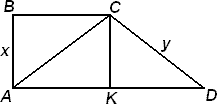 Обозначим меньшую боковую сторону за х, а большую за у (АВ<CD, т.к. наклонная всегда больше перпендикуляра).
Проведем высоту СК. Четырехугольник АВСК является прямоугольником. Как известно, в прямоугольнике противоположные стороны равны: АВ=СК=х и ВС=АК.
Определим разность оснований: AD-BC=AD-AK=KD=9
Запишем отношение боковых сторон:
х/y=4/5, откуда
y=(5/4)x Для прямоугольного треугольника CDK запишем теорему Пифагора:
CD²=CK²+KD²
у²=х²+9²
(25/16)x²=х²+81
(9/16)x²=81
x²=144
x=12

Диагональ АС явно меньше диагонали BD. Это становится ясно если сравнить прямоугольные треугольники ABD и АСК: катеты АВ и СК у них равны, а AD>AK. Поэтому АС=13.
Из прямоугольного треугольника АСК определим катет АК, используя теорему Пифагора:
АК²=АС²-СК²
АК²=13²-12²=25
АК=5
Далее
AD=AK+KD=5+9=13
BC=FR=5
Определим площадь по основной формуле площади трапеции:
S_ABCD=СК * (AD+BC)/2=12 * (13+5)/2=108