Задача №29

Дано: КАВСD - четырехугольная пирамида. К - вершина, АВСD - трапеция, причем, АВ=СD. Высота пирамиды падает в центр вписанной в основание окружности. Двугранный угол при ребре АВ равен 60°. АВ=4, ∠ВАД=30°. Найти площадь боковой поверхности пирамиды.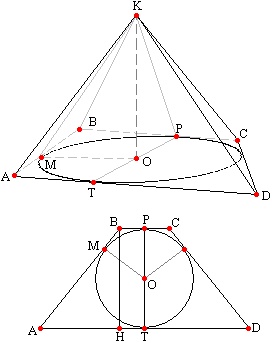
Итак, проведем радиусы вписанной в основание окружности в точки касания. Радиус, проведенный в точку касания, перпендикулярен касательной. Теперь соединим точки К и М. Прямая КМ перпендикулярна ребру АВ по теореме о трех перпендикулярах. Т.е. угол ОМК является линейным углом двугранного угла между основанием АВСD и боковой гранью АВК и равен 60 градусов.
Высота, как перпендикуляр к плоскости основания, прпедикулярна любой прямой в этой плоскости (по определению), поэтому треугольник КОМ прямоугольный.
Рассмотрим основание АВСD. Проведем высоту ВН. Из прямоугольного треугольника АВН найдем ВН:
ВН=АВ * sin30°=2.
Теорема: радиус вписанной окружности равен половине высоты. Значит, ОМ=1.
Из прямоугольного треугольника КОМ: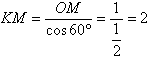

Теорема: если в четырехугольник можно вписать окружность, то суммы длин его противоположных сторон равны. Т.е. AD+BC=AB+CD=8, а периметр основания равен 16.
Для находения площади боковой поверхности пирамиды применим формулу: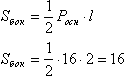