Задача №30

Основанием пирамиды KABC является правильный треугольник ABC, сторона которого равна a. Ребро KA перпендикулярно к плоскости ABC, а плоскость KBC составляет с плоскостью ABC угол в 30 градусов. Найдите площадь боковой поверхности пирамиды.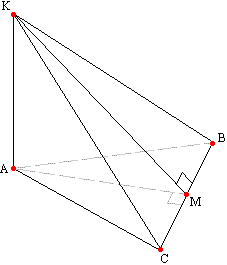
В треугольнике АВС проведем высоту АМ. По свойству о трех перпендикулярах.
Угол АМК является линейным углом двугранного угла между плоскостями АВС и КВС , поэтому ∠АМК=30°. Ребро АК перпендикулярно основанию, поэтому перпендикулярно любой прямой плоскости основания (по определению), т.е. треугольники КАС, КАМ и КАВ прямоугольные.
1. Из треугольника АВМ по теореме Пифагора найдем АМ;
2. Из треугольника КАМ найдем АК и КМ, применяя соотношения углов и сторон в прямоугольном треугольнике;
3. Найдем площади боковых граней;
4. Найдем площадь боковой поверхности: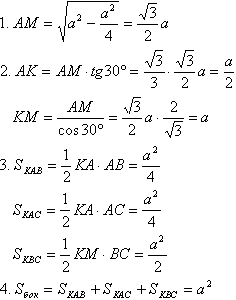