Задача №43

Отрезок АВ равен 13 см, точки А и В лежат на разных окружностях оснований цилиндра. Найдите расстояние от отрезка АВ до оси цилиндра, если его высота равна 5 см, а радиус основания равен 10 см.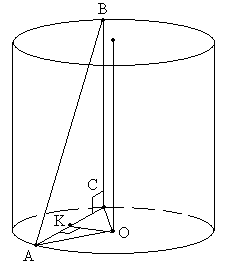


Мы видим, что АВ и ось цилиндра - скрещивающиеся прямые.
Все о скрещивающихся прямых тут, в том числе и способ и принцип нахождения расстояния между скрещивающимися прямыми.
Используя правила нахождения расстояния между ск. прямыми (которые смотрим по ссылке выше) найдем отрезок ОК являющийся расстоянием между нашими ск. прямыми АВ и осью цилиндра.
Рассмотрим треугольник АВС: в нем АВ = 13, ВС равно высоте цилиндра = 5 и он прямоугольный по построению (подробнее о прямоугольных треугольниках тут). Поэтому по теореме Пифагора находим АС = 12.
Рассмотрим треугольник ОАС: он равнобедренный ОА=ОС - радиусы основания и в нем ОК - высота опущенная на основание. Она делит основание попалам АК=КС=6.
Рассмотрим треугольник АКО: он прямоугольный и в нем АК = 6 и ОА = 10 - радиус основания цилиндра. Поэтому по теореме Пифагора определяем ОК = 8