| Главная Онлайн-расчеты Научный калькулятор | |
Задача №93В правильной треугольной пирамиде высота равна b, сторона основания равна а. Найдите угол между боковым ребром и плоскостью основания.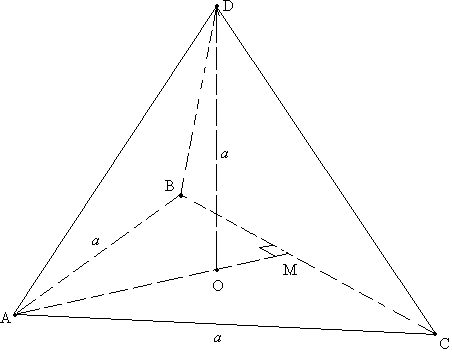 Т.к. пирамида правильная, то все ребра наклонены к основанию под одинаковым углом. Т.е. достаточно найти один из них. Например, возьмем угол при вершине А. Угол между прямой и плоскостью - угол между этой прямой и её проекцией на эту плоскость. Для нахождения проекции ребра АК на плоскость АВС проведем высоту пирамиды КО. Как известно, высота правильной пирамиды падает в центр основания. Для треугольника это пересечение медиан. Но т.к. пирамида правильная, т.е. основание правильный многоугольник, все замечательные точки совпадаю. Значит точка О является центром описанной около основания - треугольника АВС окружности. Значит, проекция ребра АК отрезок АО является также и радиусом описанной около треугольника АВС окружности. Найдем его по теореме синусов: Высота КО перпендикулярна любой прямой плоскости АВС по определению, т.е. КО^АО, значит, треугольник АКО прямоугольный. По известным катетам определим искомый угол КАО:  |
|