Задача №155

Дан треугольник АВС (АВ=ВС). АС=а, угол А=альфа. Найти:
1.АВ
2.Площадь треугольника
3.Высоты трегольника
4.Медианы треугольника
5.Биссектрисы треугольника
6.Площадь вписанной окружности
7.Площадь описанной окружности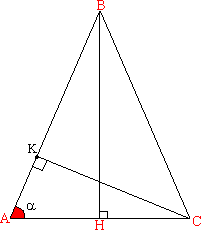
1. Проведем высоту ВН. По свойству рб.тр. эта высота является также медианой и биссектрисой. Поэтому АН=НС=а/2. Из прямоугольного треугольника АВН найдем АВ:
АВ=AH/cosα=а/2cosα
2. Вычислим площадь по формуле S=1/2absinα:
S=1/2 * а * (а/2cosα) * sinα=1/4 * а² * tgα
3. Из прямоугольного треугольника АВН найдем ВН:
ВН=AH * tgα=1/2 * а * tgα
Из прямоугольного треугольника АКС:
СК=AH * sinα
СК=a * sinα
Третья высота будет равна СК, и найти её можно аналогичным способом.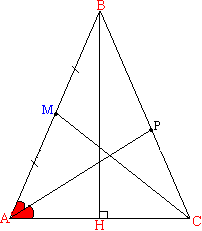
4. Для нахождения медианы СМ запишем в треугогльнике АМС теорему косинусов:

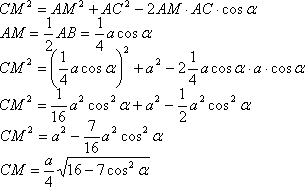третья медиана будет равна СМ, и найти её можно аналогично.
5. ∠А=∠С по теореме, которая гласит: углы при основании рб.тр. равны. ∠САР=α/2 по построению.
Из теоремы о сумме углов треугольника найдем:
∠АРС=180°-∠РАС-∠РСА=180°-α/2-α=180°-3α/2
Для нахождения биссектрисы АР вы треугольнике АРС запишем теорему синусов: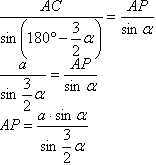

третья биссектриса будет равна АР, и найти её можно аналогично.
Для выполнения пунктов 6. и 7. задания подставим известное в соответствующие формулы: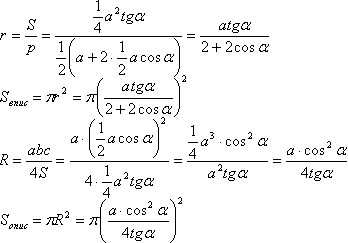