| Главная Онлайн-расчеты Научный калькулятор | |
Задача №238Дан треугольник АВС со сторонами ВС=17, АС=21, АВ=10. Найдите радиус окружности, проходящей через вершины А и В, центр которой находится на высоте BD.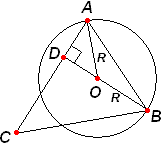 1. Определим площадь треугольника по формуле Герона: p=24; р-а=7; p-b=3; р-с=14 S=84 2. Теперь, используя формулу S=ah площади треугольника определим высоту BD: BD=2S/AC=8 3. Из прямоугольного треугольника АВD по теореме Пифагора определим катет AD: AD2=AB2-BD2 AD2=100-64=36 AD=6 4. Соединим точки О и А. Обозначим радиус окружности за R (АО=ВО=R). Значит, OD=BD-OB=8-R. Запишем для прямоугольного треугольника АОD теорему Пифагора: АО2=AD2+OD2 R2=62+(8-R)2 R2=36+64-16R+R2 16R=100 R=25/4 |
|